Making the Most of Bitcoin
Epistemic status: I believe I’m drawing on common wisdom up to part 5. After that I’m just making shit up, but in a possibly interesting way. Not proper financial advice, see the end of the post.
So let’s say you have some Bitcoin. What do you do with it?
#1. Cash out everything immediately
Lots of people think putting your money in Bitcoin is a bad idea: Jack Bogle (founder of Vanguard), Warren Buffet, Robert Shiller (Yale economic professor), Mr. Money Mustache, Jason Calacanis (Angel investor)[1]. I tend to agree with them[2], and am basically following this action by not buying in[3].
However, you (hypothetical Bitcoin holder) already knew that Bitcoin was widely thought to be not the greatest investment vehicle, and bought in anyways. You’re not going to immediately cash out, ok, fine, whatever. What else could you do?
#2. Become a HODLR
You’re going to HODL the Bitcoin you have until it reaches THE MOON. It’s unclear what you’ll do once it reaches THE MOON. Maybe you’ll just slowly squander your satoshis on breeding Shiba Inus and kidnapping cryptography experts to ensure the sanctity of SHA-256.
Or maybe one day you’ll end up with 99% of your net worth in Bitcoin, and the next day you’ll have 0% of your net worth in Bitcoin because your kidnapping orders were read incorrectly, and SHA-256 was demonstrably broken by vendetta-driven cryptographers overnight[4]. Also, the Iranians are really mad at you[5].
Another way of looking at it is that it’s difficult to make money slowly with Bitcoin: there are no fundamentals[6] to inexorably drive value, you can’t yell “gains through trade, buy ’em all and let the market sort em’ out!” and put your money in an index fund equivalent and then forget about it.
The life of a HODLR is a life with a hell of a lot of volatility; maybe there’s a better strategy?
#3. Time the market
The key is to buy low, sell high. This advice is approximately as useful as “be attractive, don’t be unattractive” labeled as dating advice.
If you think you can beat the market, I’ll point you to all the rest of the brilliant ideas that have been tried and failed, and the anti-inductive nature of the market, and the seeming adequacy of liquid markets. If you still think you have a grand insight into market mechanics, the great thing is that you can go make a billion dollars if you’re right. Go on, and try to remember us little people.
Besides, if I knew how to do this, would I be here telling you? I would be out playing with my Shiba herd instead.
#4. Recoup your investment
This strategy has the virtue of simplicity:
- Buy some Bitcoin.
- Wait until the price of Bitcoin doubles.
- Sell half your Bitcoin, making back your original “investment”. Now it’s not possible to be worse off than before.
- … HODL?
It’s nice to not lose money (as long as the market doesn’t crash out before you reach your doubled price), but you have one point at which you cash out, and then you’re back to not having any strategy.
#5. Rebalance
Another strategy is to simply rebalance.
A quick tutorial detour: let’s say there are only 2 investments in the world, boonds and stoocks[7]. Boonds are low risk, low reward, and stoocks are large risk, large reward.
Let’s say you’re a young’un that has just entered the job market with $1000 to put into the market, and have an appetite for risk in order to get good returns. That means taking on higher risk, but that’s okay since you’ll have plenty of years to rebuild if things go south. So you might go for a 90% stoocks, 10% boonds allocation, for $900 stoocks/$100 boonds.
Now let’s say that the market absolutely tanks tomorrow. Boonds don’t really change since they’re low risk; let’s say boonds take a 10% hit. But stoocks, man, they took a 95% hit. Now we’ve ended up $45 stoocks/$90 boonds, meaning our asset allocation is 33.3% stoocks/66.6% boonds. #1. This is super sad, we’ve lost a lot of money, but #2. This isn’t what we want at all! We have so many boonds that our risk of losing most of what we have is low, but our returns are also going to be super low. Besides, even if we do lose it all, we’ll make it back in salary over a few days.
So what we can do is rebalance: we sell our abundance of boonds, and buy more stoocks, until we have a 90% stoock/10% boond allocation again, which works out to $121.5 stoocks/$13.5 boonds[8].
To fill out the rebalancing example, now let’s say you’re older and about to retire. Over the years you’ve shifted your asset allocation to 10% stoocks/90% boonds with $100000 stoocks/$900000 boonds: this close to retirement, you’d be in a lot of trouble if most of your money disappeared overnight, so you want low risk.
Now let’s say stoocks do fantastically well tomorrow, growing 10000%, so you end up with $10000000 stoocks/$900000 boonds. The problem is that now your allocation by percentage is 91.7% stoocks/8.3% boonds, and you’re about to enter retirement. All your wealth is in a super-risky investment! Could your heart even handle the bottom of the market dropping out? Instead of letting that happen, you could rebalance back to 10% stoocks/90% boonds or $1090000 stoocks/$9810000 boonds[9].
What’s the moral of the story? If you have multiple asset risk classes, then you don’t have to put it all on black and ride the bubbles up and down like a cowboy: rebalancing is a simple strategy to target some amount of risk, and then you can just go long and not worry about the fine details.
There are finer details that do matter: you can’t rebalance Bitcoin often or you might get eaten alive by mining fees[10] (which peaked at an average of $50 when Bitcoin was around $10000). So maybe you’d target some large-ish percentage change and only rebalance once Bitcoin changes by that amount.
Let’s run some numbers: let’s say 1 Bitcoin is currently $1000,
and you have exactly 1 bitcoin, and you rebalance only whenever Bitcoin doubles in price (this basically extends the previous “double and sell” strategy). Now if Bitcoin goes from $1000 to $10000, you would rebalance 3 times: when Bitcoin is $2000, $4000, and $8000. If you have many more assets than $1000, you can hand wave away the exact percentage calculations and just sell half the Bitcoin at each point. Even if Bitcoin crashes to $0.001 after reaching $10000, you’ve “made” $3000 that you’ve rebalanced to other stabler assets (minus fees, $~70). Not bad for riding a speculative bubble!
#6. Kind of rebalance-ish
On the other hand, only getting $3000 out of a maximum of $10000 Bitcoin seems… not a good show. Sure, you were going to get only $0.001 if you were a HODLR, but that $10000 is a juicy number, and $3000 is an awful lot smaller.
Or consider the scenario in which you read Gwern in 2011 speculating
that Bitcoin could reach $10000, and you were convinced that you should be long on Bitcoin. However, it was still possible that Bitcoin wouldn’t reach $10000, falling prey to some unforeseen problem before then. You would want to hedge, but rebalancing would throw away most of your gains before you got close to $10000. For example, if you started with $1000 @$1/BTC for a total of 1000 BTC, and you rebalanced at every doubling, you would end up with $13000 cash and ~$1000 BTC, compared to HODLing ending up with $10000000 in BTC. It’s a used car versus being the Pineapple Fund guy, I get it, it’s why HODLing is enticing.
The problem is that rebalancing doesn’t know anything about beliefs about long term outcomes, just about overall asset class volatility.
That said, if it’s possible to encode your beliefs as a probability distribution[11], you could run (appropriately named) Monte Carlo simulations of different selling strategies and see how they do, choosing a strategy that does well given what you expect the price of BTC to do.
I’ll work some simple examples, following some assumptions:
- we start from a current price of $10000/BTC.
- we don’t care about the day-to-day price: if BTC reaches $20000, dips back to $15000, and then rises to $50000, we aren’t concerning ourselves with trying to time the dip, just with the notion that BTC went from $20000 to $50000.
- rebalancing is replaced with a hedge operation, where some fixed fraction of our Bitcoin stake is sold, at some fixed rising proportion of BTC. We’ll fix our sell point at every doubling (except for a sensitivity analysis step below).
- the transfer fees are set to be proportional to the price of BTC, at 0.5%: in practice, this just serves as a drag on the BTC-cash conversion. If you’re dealing with amounts much larger than 1 BTC (or SegWit works out), you might be able to amortize the transfer costs down to 0. To allow interpolating between both cases, we’ll simply give both 0.5% and 0% transaction drag simulations.
- the price of Bitcoin is modeled as rising to some maximum amount, and then crashing to basically nothing. This can also cover cases where BTC crashes and stays low for such a long time that it would have been better to put your assets elsewhere.
The processes of adapting the general principle to real life, consulting the economic/finance literature for vastly superior modeling methods, using more sophisticated selling strategies than selling a constant fraction, and not betting your shirt on black is left as an exercise to the reader.
So let’s say our beliefs are described by a mangled normal distribution[12]: we’re certain BTC will reach the starting price (obviously, we’re already there), around 68% less certain BTC will reach 1 standard deviation above the starting price, 95% less certain BTC will reach the 2nd standard deviation, so on and so forth. We’re not interested in a max BTC price below our starting price, so we’re just chopping the distribution in half and doubling the positive side.
Since we’ve centered the normal distribution on our starting price, we have only one other parameter to choose, our standard deviation (stdev). Some values are obviously bad: choosing a stdev of $1 means you are astronomically confident that BTC will never go above $10100. While you might not believe in the fundamentals behind Bitcoin, it is odd to be so confident that the crash is going to happen in such a specific range of prices. On the other hand, I don’t have a formal inference engine from which I can get a stdev value that best fits my beliefs, so I’ll be generous and choose a middling value of $10000.
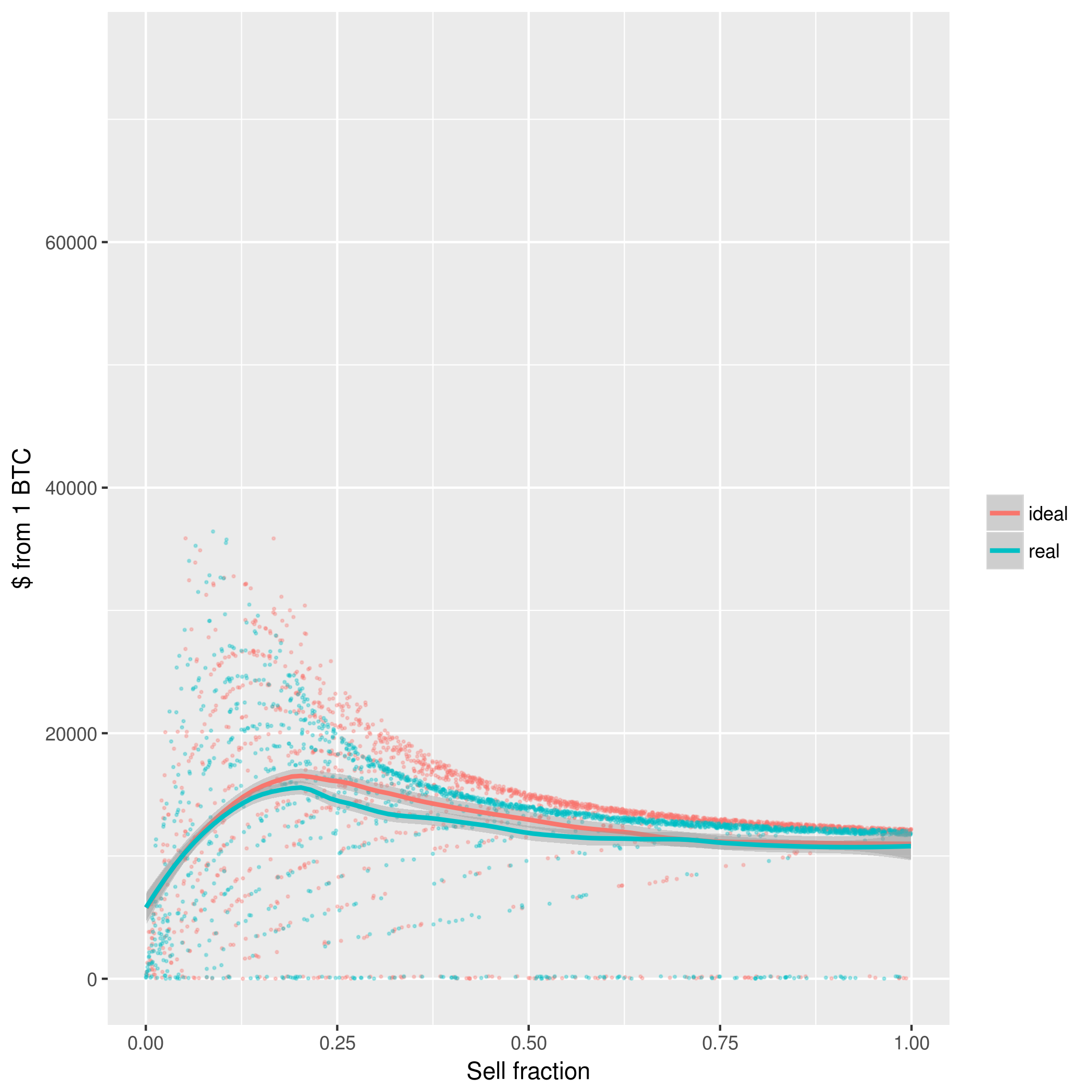
So if we run a number of simulations where the price of BTC follows the described normal distribution, we get:

Several things become apparent right away:
- there’s an obvious stepping effect happening[13]. Thinking about it, it’s obvious that each separate line is describing the effects of selling at each doubling. The lowest line only manages to sell once, the next line sells twice, and so on.
- as one might expect, selling everything is low variance, and holding more is higher variance. As a reference point, the 0.5 sell fraction is just the previously described rebalancing strategy.
- even when hitting 4 sell points, the transaction drag on 1 BTC isn’t too bad.
- fitting a trend line with LOESS gets us a rough[14] measure of expected profit. In particular, we seem to top out at $20000 around a 0.5 sell fraction.
An obvious sensitivity analysis comes to mind: does the fact we’re selling only at every doubling matter? What if we sold more often? We can re-run the analysis when we sell at every 1.2x:
The stepping effect is still there, but less obvious: we hit more steps on the way to the crash price. The largest data points don’t go as high, but you can also see fewer zero values, since we pick up some selling points between $10000 and $20000. Additionally, the LOESS peaks at a lower sell fraction, which makes some sense: since we’re hitting more sell points, we can afford to hold on to more.
What if the normal distribution doesn’t describe our beliefs? Say we want more emphasis on the long term. Then our beliefs might be better modeled with the exponential distribution which is known to have a thicker tail than the normal.
If we use $10000 for the exponential distribution’s lambda parameter, then our simulations look like:

The behavior isn’t too different, with the exception that some simulations start surviving to the 5th sell point. Additionally, the LOESS curves move to the left a bit compared to the normal, but only by a little: from eyeballing it, the peak might move from a sell fraction of 0.55 to 0.45.
Again, there are more sophisticated analyses; for example, maybe you think that your probability distribution peaks around $100k/BTC and falls off to either side, in which case you would want a more complicated strategy to take advantage of your more complicated beliefs.
However, there’s a theoretical problem with our analyses thus far. The distributions we’ve been using are unbounded, allowing BTC prices that can theoretically go to infinity. Sure, we can treat economics as effectively unbounded: there sure are a lot of stars out there, and no economic activity has even left Earth orbit (Starman, some bacteria, and drawings of naked people notwithstanding). But that’s in the long run[15], and we only really care about BTC in the short term, when it’s generating “returns” in excess of normal market returns. For example, if BTC is wildly successful and becomes the world currency, it becomes hard to see how BTC can continue to grow in value far beyond the economic growth of the rest of the world[16]. So we might assume that once BTC eats the world, BTC just follows the bog standard economic growth of the world, and ceases to be interesting relative to all other assets[17].
However, this does mean we can add two assumptions: our distributions should be bounded, and there’s a chance the value of our held BTC doesn’t all disappear in the end. I’ll bound our distributions at the current stock market cap (as of 2018/03/06 $80 trillion, rounded to $100 trillion for ease of math)[18], and use a 2nd function (not a probability distribution!) to encode the probability that if BTC reaches a certain price, it will crash.
For the probability of reaching a price, I’ll keep using the exponential distribution, but bounded and re-normalized to add up to 1 within the bounds[19]. For the probability that BTC will crash, we don’t need a distribution: we could imagine a function that always returns 100% for a crash (as we were before), or 0, or any value between. Mathematically importantly, we’re not beholden to normalization concerns. I essentially free handed this function piecemeal with polynomials, with the goal of reflecting a belief that either BTC stabilizes as a small player in the financial markets, or becomes the world currency and not likely to lose value suddenly. Plotted on log axes:

When we run simulations (displayed on a log y-axis):

Up to now transaction drag hasn’t been such a big deal, but it suddenly shows up as a big deal: if we end up in a world where the price of BTC goes long and retains value, 0.5% drag appears to suddenly be super important, preventing us from getting close to the maximum $10000000 from our initial 1 BTC. It’s not too surprising, since more mundane investments need to also deal with fee[20] and tax drag.
But if these beliefs are correct, do we do better on average? Not really, especially with transaction drag factored in. This holds true even when we zoom in on a linear axis[21][22]:
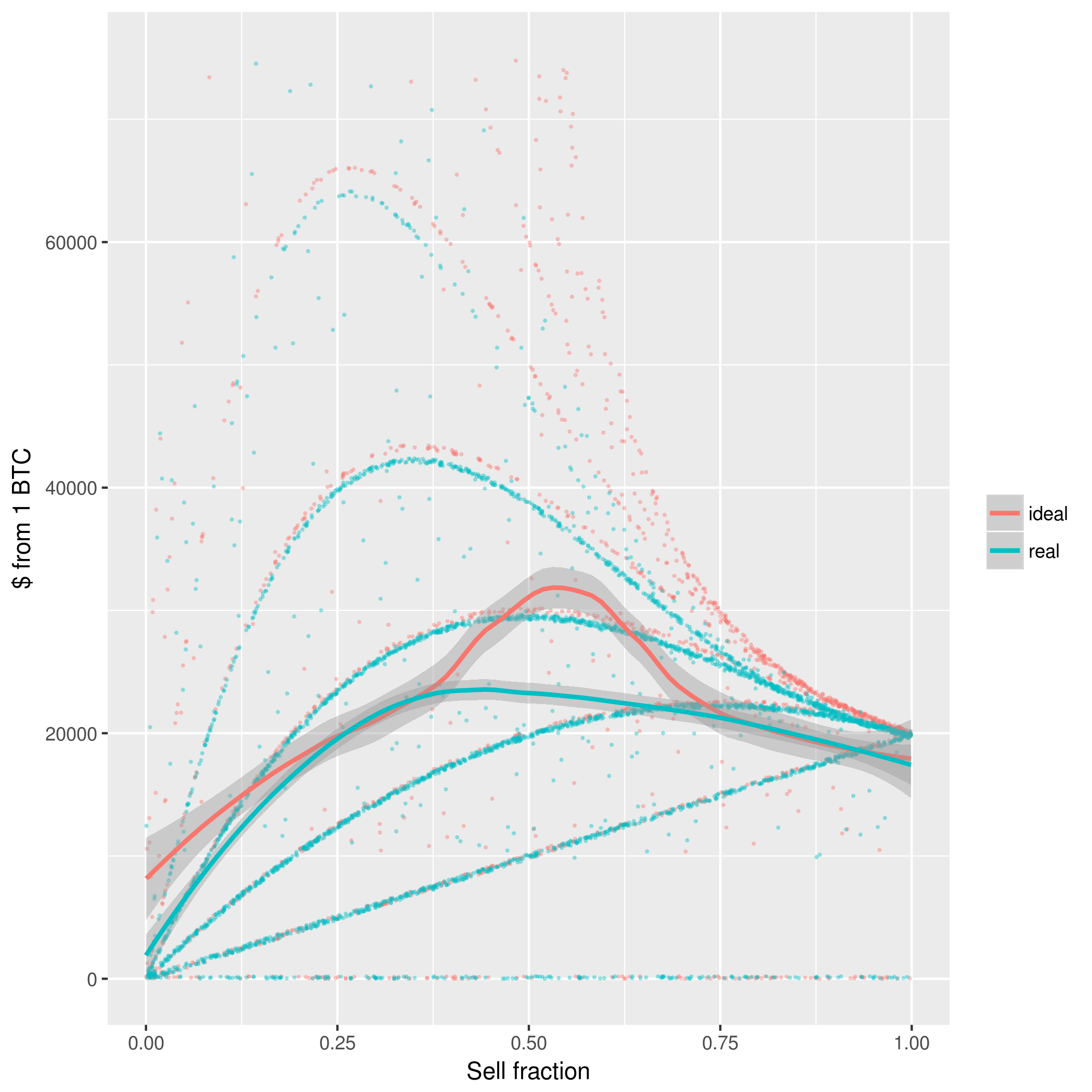
I’ll end here. You could always make your models more complicated, but I’m making precisely $0 off this and that XCOM 2 isn’t going to play itself.
So after all this analysis, what do I recommend you do?
Trick question! I don’t recommend you do anything, because this post is not financial advice. If you persist in trying to take financial advice from someone who may frankly be a corgi, the world will laugh at you when BTC crashes to the floor and Dogecoin rises to take it’s place as the true master of cryptocurrencies. ALL HAIL THE SHIBA, WOOF WOOF.
R code used to generate the graphs available on github.
[1] ↑ “But all those people are famous and invested in the status quo!” Okay, you got me, will linking to a non-super-rich acquaintance’s opinion on Bitcoin help?
To be even fairer, I could also come up with a similar list supporting Bitcoin instead, but I’m less interested in debating the merits of Bitcoin, and more interested in what you do once you wake up with a hangover and a wallet full of satoshis.
[2] ↑ I disagree with Scott when he says that we should have won bigger with Bitcoin. Most of the gnashing of teeth over Bitcoin is pure hindsight bias.
[3] ↑ Currently the only reason I would get any cryptocurrency is to use it as a distributed timestamping service.
[4] ↑ It’s not just breaking the base crypto layer: the nations of the world could decide to get real and criminalize Bitcoin. Law enforcement could get better at deanonymizing transactions, causing all the criminals to leave for something like Monero. Price stabilization just never happens, and people get sick of waiting for it to happen. Transaction fees spike whenever people actually try to use Bitcoin as a currency, or the Lightning Network turns out to have deep technical problems after a mighty effort to put it into place (deep problems in a widely deployed technology? That could never happen!). Ethereum gets its shit together and eats Bitcoin’s lunch with digital kittens. There’s the first mtgox-level hack since BTC started trading on actual exchanges. People decide they want to cash out of the tulip market en masse (although that might be unfair to the tulips).
[5] ↑ It’s unclear where you would get a Shah today, but exhuming all past Shahs is probably enough to piss people off.
[6] ↑ No, evading taxes/police actions is not a fundamental.
[7] ↑ Names munged to emphasize that they’re fantasy financial instruments.
[8] ↑ There’s something to be said about keeping a stable and liquid store like a savings account to make sure living expenses are covered for 6 months. You can replace the implied “all assets” with “all available assets” for a more non-toy policy.
[9] ↑ If the market simply dropped back to its previous position before you could rebalance, then you aren’t any worse off than you were 2 days ago, so maybe it wouldn’t be so disappointing to miss this opportunity. But that’s just anchoring, and Homo Economicus in your position would be super bummed.
[10] ↑ Normal investments have similar tax implications where you realize gains/losses at sale, covered by the general term tax drag.
[11] ↑ More on probabilities as states of beliefs, instead of simply reflecting experimental frequencies.
[12] ↑ Coming up with a better distribution is left as an exercise for the reader.
[13] ↑ A mild amount of jittering was added to make this visible with more simulation points.
[14] ↑ LOESS fits with squared loss, which emphasizes outliers, which you might not want. Additionally, LOESS is an ad hoc computational method (much like k-means) which won’t necessarily maximize anything; the main advantage is that it looks pretty if you choose the right spans to average over, and you don’t have to come up with a parametric model to fit to.
[15] ↑ And as they say, in the long run we’re all dead. Yes, we’re working on that.
[16] ↑ Sure, the bubble could continue, but bubbles pop at some point, and if it’s so damn important to the economy war isn’t out of the question, and if large scale nuclear war happens, more than just the price of Bitcoin is going to crash. “Here lies humanity: they committed suicide by hard math.”
Or a different perspective. Who would win?
- Billions of people that didn’t buy into Bitcoin, all frozen out of the brave new economy, backed by all the military might of nations that care about the sovereignty of their money supply.
- One chainy boi.
[17] ↑ There’s reasons to believe BTC might act otherwise:
- The fact that Bitcoin is deflationary, so it probably won’t act like a normal commodity in the limit if it eats the world. Even companies can issue more stock, or more gold found.
- The marginal Bitcoin might be way over priced forever.
[18] ↑ Interestingly, this implies that BTC only has around 1000x of hyper-growth headroom.
[19] ↑ The distribution chart is not properly normalized, since the distribution is actually linear without the log axis, but it simulates correctly.
[20] ↑ The movement to index funds seems partly rooted in avoiding high mutual fund fees.
[21] ↑ I’m not entirely sure what that hump in the ideal price is doing: it shows up in the other LOESS curves, and persists with changes in the random seed.
[22] ↑ We end up with a different maximum hump with the log and linear graphs: what’s going on here? Keep in mind that LOESS operates on minimizing squared error, and minimizing squared log error is a bit different than minimizing squared error.